Modulo A % B
Calculate the remainder after dividing one numeric value
The Modulo A % B block in the GraphLinq IDE is a versatile mathematical block used to calculate the remainder after dividing one numeric value (A) by another (B). This block is particularly useful for handling cyclic or repetitive patterns, as well as determining even or odd numbers.
Block Description
The Modulo A % B block belongs to the Math blocks category in the GraphLinq IDE. Like other blocks in this category, it is a non-executive block, meaning it does not have yellow connectors and is implicitly called when its output is needed by other blocks during graph execution.
Input Parameters
The Modulo A % B block requires two input parameters:
A (Numeric Type): The A input represents the dividend or the numeric value from which the remainder is calculated.
B (Numeric Type): The B input is the divisor, representing the numeric value used to divide A and calculate the remainder.
Both A and B inputs accept various numeric data types, such as decimals, integers, and longs. It is essential to ensure that the B input is not set to zero, as division by zero is undefined and may result in errors in the graph's execution.
Output
The Modulo A % B block outputs the remainder obtained by dividing the value of input A by the value of input B. The output is of the same data type as the inputs and represents the result of the modulo operation.
Example Use Case
Let's explore a practical example of how the Modulo A % B block can be used within a graph:
The graph receives a series of timestamp values (A) representing events.
The Modulo A % B block is called, taking the timestamp values (A) as the dividend and a fixed value (B), such as 24, as the divisor.
The block calculates the remainder when each timestamp is divided by 24, representing the hours of the day.
The output represents the hours of the day (0 to 23) for each event timestamp, indicating the occurrence of events within different hours.
In this example, the Modulo A % B block helps identify the cyclic pattern of events throughout the day, providing valuable insights into the timing and frequency of occurrences.
Conclusion
The Modulo A % B block is a valuable mathematical tool in the GraphLinq IDE, enabling developers to perform modulo operations and extract remainders from numeric values. Its versatility makes it suitable for various applications, including time-related calculations, periodic event analysis, and determining even or odd numbers. By leveraging the Modulo A % B block, developers can efficiently handle cyclic patterns and gain valuable information from numeric data within their graphs.
More Information
The Modulo A % B block in the GraphLinq IDE performs the modulo operation on two given numeric values "A" and "B." The modulo operation calculates the remainder after dividing "A" by "B." This block is useful for obtaining the remainder of a division and is particularly relevant in scenarios where repetitive patterns or cyclical behaviors need to be identified.
Block Details
The Modulo A % B block has two input parameters, "A" and "B," representing the numeric values for which the modulo operation is to be performed. Both "A" and "B" can be of various numeric data types, such as decimal, integer, or long.
Execution
As with other block types in the Math category, the Modulo A % B block is non-executive. It does not have yellow connectors and is implicitly called whenever its output is needed as input by other executing blocks. When the Modulo A % B block's output is required in a graph, it performs the modulo operation on the input values "A" and "B" and provides the remainder as output.
Use Case
The Modulo A % B block finds applications in various fields, including computer programming, finance, and cryptography. In computer programming, it is used for tasks such as checking if a number is even or odd, generating random numbers with a specific range, and implementing algorithms for handling cyclical behaviors or circular data structures.
Example
Let's consider an example to illustrate the usage of the Modulo A % B block. Suppose we have a graph that simulates a clock with hours, minutes, and seconds. The graph takes the total number of seconds as input and needs to calculate the equivalent time in hours, minutes, and remaining seconds.
To achieve this, we can use the Modulo A % B block. First, we divide the total number of seconds by 3600 (the number of seconds in an hour) to calculate the hours. Then, we take the remainder after this division using the Modulo A % B block to find the remaining seconds. Next, we divide this remainder by 60 (the number of seconds in a minute) to calculate the minutes.
By using the Modulo A % B block, we can efficiently determine the cyclical components of the clock, ensuring that the time representation is accurate and conforms to the conventional time format.
The Modulo A % B block's ability to calculate remainders is invaluable in various scenarios where cyclical or repetitive patterns need to be analyzed or managed. It offers developers a powerful tool for handling modulo operations within their graphs, contributing to the versatility and functionality of their applications.
Full Example
Modulo A % B blocks output the result of a modulo operation* of two given numbers.
As you might imagine, Modulo A % B blocks have two input parameters called "A" and "B". In the division that determines the output of the modulo operation, "A" is the numerator and "B" is the denominator. Both of these input parameters should be of the integer data type.
One of the most common uses of the modulo operator is as a divisibility check for the purpose of tracking every nth instance of something. For example, say we want to detect programatically if we are in a fiscal quarter end month. Those happen every 3 months; in other words, they happen in every month whose number is divisible by 3. Whenever a number is divisible by another, the result of the first number % the second number will always be 0. So, we can simply check if [current month] % 3 is equal to 0. If so, then we are in a fiscal quarter end month (3, 6, 9, or 12).
We use a similar technique in the graph below to detect every 100th Bitcoin block added to the chain:
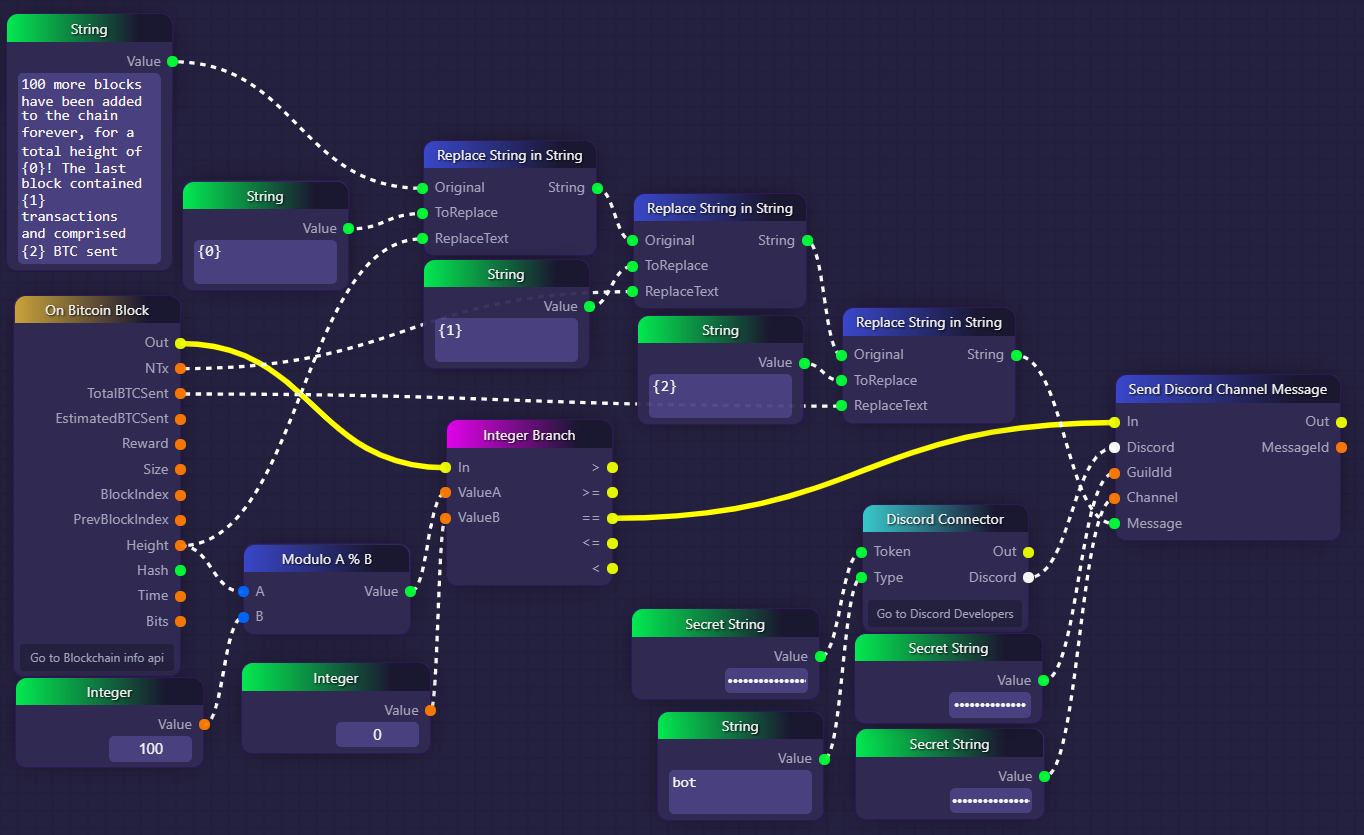
In the example above, we use a Discord bot to send a message in a Discord channel that contains some data about the most recent Bitcoin block (the block height, the number of transactions, and the amount transacted). However, we don't want this to happen for every single Bitcoin block, as there are about 6 blocks added every hour, and we don't want to flood our Discord channel with 150 messages each day about new blocks. Instead, we would like to send these Discord notifications only for every 100th block added, so that our channel will be updated about Bitcoin block production only once or twice a day, which is much more reasonable.
The On Bitcoin Block event block will fire every time a new Bitcoin block is added to the chain. The "Height" output parameter represents the total amount of blocks on the Bitcoin chain (ie: the block number for the most recent block). If we take the modulo of that number and 100, the result will be 0 only when the block height is some multiple of 100, like 500, 6000, or 765400
So, we use our Modulo A % B block to calculate the modulo between the current block height and the number 100, and then we use an Integer Branch to check if the result equals 0; only if it does do we proceed to build and send our Discord message. So, the Integer Branch the block will only call the Send Discord Channel Message block once for every 100 times that the On Bitcoin Block event fires, thanks to our modulo check.
Whenever the block height does happen to be a multiple of 100, then we simply use a chain of Replace String In String blocks to build a message string containing the data we're interested in, and then send it to our Discord channel via some bot we control using a Send Discord Channel Message block.
*Modulo (%) operations are arithmetic operations between two operands that return the remainder after a division of the first operand by the second. For example, 7 % 3 = 1, because 3 fits into 7 2 full times, which leaves a remainder of 1. This operation is often used to determine if given numbers are even or odd, multiples/factors of other numbers, or prime.
Last updated
